أول أمر خطي المعادلة التفاضلية الشكل التالي :

The general solution is given by الحل هو العام الذي قدمته

where أين

called the integrating factor . ووصف دمج عامل. If an initial condition is given, use it to find the constant C . وإذا كان الشرط هو إعطاء الأولية ، واستخدامها لإيجاد المستمر جيم.
Here are some practical steps to follow: وإليك بعض الخطوات العملية التالية :
1. 1.
If the differential equation is given as إذا كانت المعادلة التفاضلية يرد
 , ،
, ، rewrite it in the form إعادة كتابة ذلك في شكل
 , ،
, ، where أين

2. 2.
Find the integrating factor العثور على عامل دمج
 . .
. . 3. 3.
Evaluate the integral تقييم متكاملة

4. 4.
Write down the general solution أكتب حل العامة
 . .
. . 5. 5.
If you are given an IVP, use the initial condition to find the constant C . إذا كنت أعطي IVP استخدام الشرط الأولي لإيجاد المستمر جيم.
Example: Find the particular solution of: مثال : ابحث عن حل وخصوصا :

Solution: Let us use the steps: الحل : فلنستعمل الخطوات التالية :
Step 1: There is no need for rewriting the differential equation. الخطوة 1 : ليس هناك حاجة لإعادة صياغة المعادلة التفاضلية. We have لدينا

Step 2: Integrating factor الخطوة 2 : دمج عامل
 . .
. . Step 3: We have الخطوة 3 : لقد
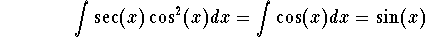 . .
. . Step 4: The general solution is given by الخطوة 4 : الحل العامة التي تقدمها
 . .
. . Step 5: In order to find the particular solution to the given IVP, we use the initial condition to find C . الخطوة 5 : من أجل التوصل إلى حل لا سيما في ضوء IVP نستخدم الشرط الأولي لايجاد جيم. Indeed, we have في الواقع ، لدينا
 . .
. . Therefore the solution is ولذلك فإن الحل
 . .
. . Note that you may not have to do the last step if you are asked to find the general solution (not an IVP). ملاحظة أنه لا يمكنك أن تفعل يكون الخطوة الأخيرة إذا طلب منك لإيجاد حل العامة (ليست IVP).
If you would like more practice, click on Example . إذا كنت تود الحصول على مزيد من الممارسة العملية ، اضغط على مثال.
مثال : ابحث عن حل
 . .
. . Solution. الحل.
الحل : أولا ، نحن نعترف بأن هذا هو خطي المعادلة. Indeed, we have في الواقع ، لدينا

Therefore, the integrating factor is given by ولذلك ، فإن دمج عامل المقدمة
 . .
. . Since منذ
 , we get نحصل
, we get نحصل 
Hence, the general solution is given by the formula ومن ثم ، فإن الحل هو عام للصيغة التي قدمتها

We have لدينا

The details for this calculation involve the technique of integrating rational functions . تفاصيل هذا الحساب لتشمل تقنية دمج مهام الرشيد. We have لدينا

Hence, the only difficulty is in the integral ومن ثم ، فإن الصعوبة الوحيدة هي في يتجزأ
 . Here we will use integration by parts . وهنا سوف نستخدم التكامل أجزاء. We will differentiate t and integrate علينا التفريق بين طن وتكامل
. Here we will use integration by parts . وهنا سوف نستخدم التكامل أجزاء. We will differentiate t and integrate علينا التفريق بين طن وتكامل  . . The details are left to the reader. التفاصيل متروكة للقارئ. We have لدينا
. . The details are left to the reader. التفاصيل متروكة للقارئ. We have لدينا 
Therefore, we have لذلك ، لدينا
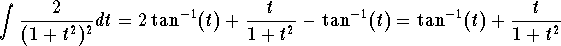 , ،
, ، which clearly implies مما يعني بوضوح

The general solution can also be rewritten as عموما الحل كما يمكن إعادة صياغة النحو
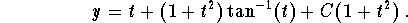
Finally, the initial condition y (0) = 0.4 gives C = 0.4. وأخيرا ، فإن الشرط الأولي ذ (0) = 0.4 = 0.4 يعطي جيم. Therefore, the solution to the IVP is ولذا ، فإن الحل هو لIVP

منقول من موقع رياضيات العالم











