المعادلة التفاضلية للشكل  is called separable , if f ( x , y ) = h ( x ) g ( y ); that is, ويسمى فصل ، إذا و (خ ، ذ) ح = (س) ز (ذ) وهذا هو ،
is called separable , if f ( x , y ) = h ( x ) g ( y ); that is, ويسمى فصل ، إذا و (خ ، ذ) ح = (س) ز (ذ) وهذا هو ،

In order to solve it, perform the following steps: من أجل إيجاد حل لها ، والقيام بالخطوات التالية :
(1) (1)
Solve the equation g ( y ) = 0, which gives the constant solutions of ( S ); حل المعادلة ز (ذ) = 0 ، والذي يعطي حلولا ثابتة من (س) ؛
(2) (2)
Rewrite the equation ( S ) as إعادة كتابة المعادلة (د)
 , ،
, ،
and, then, integrate وإذن ، دمج

to obtain للحصول على

(3) (3)
Write down all the solutions; the constant ones obtained from (1) and the ones given in (2); أكتب كل الحلول ؛ المستمر التي تم الحصول عليها من (1) وتلك الواردة في (2) ؛
(4) (4)
If you are given an IVP, use the initial condition to find the particular solution. إذا كنت أعطي IVP استخدام الشرط الأولي للعثور على حل. Note that it may happen that the particular solution is one of the constant solutions given in (1). لاحظ أن ذلك قد يحدث وخصوصا ان الحل هو واحد من حلول ثابتة في (1). This is why Step 3 is important. ولهذا السبب من المهم الخطوة 3.
Example: Find the particular solution of مثال : ابحث عن حل لل
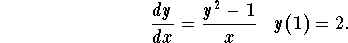
Solution: Perform the following steps: الحل : القيام بالخطوات التالية :
(1) (1)
In order to find the constant solutions, solve من أجل إيجاد حلول المستمر ، لحل . We obtain y = 1 and y =-1. ونحن في الحصول على ذ و ذ = 1 =- 1.
. We obtain y = 1 and y =-1. ونحن في الحصول على ذ و ذ = 1 =- 1.
(2) (2)
Rewrite the equation as إعادة صياغة المعادلة على النحو
 . .
. .
Using the techniques of integration of rational functions , we get باستخدام تقنيات التكامل العقلاني وظائف ، نحصل
 , ،
, ،
which implies وهو ما يعني ضمنا

(3) (3)
The solutions to the given differential equation are فإن التوصل إلى حلول في ضوء المعادلة التفاضلية

(4) (4)
Since the constant solutions do not satisfy the initial condition, we are left to find the particular solution among the ones found in (2), that is we need to find the constant C . منذ حلول ثابتة لا تستوفي الشرط الأولي ، فإننا نجد على اليسار وخصوصا تلك التي بين الحل وجدت في (2) ، والتي نحن في حاجة إلى إيجاد المستمر جيم. If we plug in the condition y =2 when x =1, we get إذا كنا في حالة سد ذ = 2 س = 1 عندما نحصل
 . .
. .
Note that this solution is given in an implicit form. علما أن هذا الحل هو في شكل ضمني. You may be asked to rewrite it in an explicit one. قد يطلب منك إعادة كتابة ذلك في واحدة واضحة. For example, in this case, we have على سبيل المثال ، في هذه الحالة ، لدينا

If you would like more practice, click on Example . إذا كنت تود الحصول على مزيد من الممارسة العملية ، اضغط على مثال.
مثال : البحث عن حلول
 . .
. .
Solution: First, we look for the constant solutions, that is, we look for the roots of الحل : أولا ، نحن نبحث عن حلول ثابتة ، أي أن علينا أن نبحث عن جذور

This equation does not have real roots. هذه المعادلة ليس لها جذور حقيقية. Therefore, we do not have constant solutions. ولذلك ، ليس لدينا حلول ثابتة.
The next step will be to look for the non-constant solutions. وستكون الخطوة التالية هي البحث عن حلول غير ثابتة. We proceed by separating the two variables to get نشرع بفصل اثنين من المتغيرات للحصول على
 . .
. .
Then we integrate ثم ندمج

Since منذ
 = =
= =  = 1 - = 1 --
= 1 - = 1 -- 
we get نحصل

Therefore, we have لذلك ، لدينا

It is not easy to obtain y as a function of t , meaning finding y in an explicit form. فليس من السهل الحصول على ذ كوظيفة من وظائف طن ، مما يعني إيجاد ذ بشكل صريح.
Finally, because there are no constant solutions, all the solutions are given by the implicit equation وأخيرا ، لأنه لا توجد حلول ثابتة ، وجميع الحلول التي قدمها ضمنية المعادلة

منقول من موقع رياضيات العالم
 is called separable , if f ( x , y ) = h ( x ) g ( y ); that is, ويسمى فصل ، إذا و (خ ، ذ) ح = (س) ز (ذ) وهذا هو ،
is called separable , if f ( x , y ) = h ( x ) g ( y ); that is, ويسمى فصل ، إذا و (خ ، ذ) ح = (س) ز (ذ) وهذا هو ، 
In order to solve it, perform the following steps: من أجل إيجاد حل لها ، والقيام بالخطوات التالية :
(1) (1)
Solve the equation g ( y ) = 0, which gives the constant solutions of ( S ); حل المعادلة ز (ذ) = 0 ، والذي يعطي حلولا ثابتة من (س) ؛
(2) (2)
Rewrite the equation ( S ) as إعادة كتابة المعادلة (د)
 , ،
, ، and, then, integrate وإذن ، دمج

to obtain للحصول على

(3) (3)
Write down all the solutions; the constant ones obtained from (1) and the ones given in (2); أكتب كل الحلول ؛ المستمر التي تم الحصول عليها من (1) وتلك الواردة في (2) ؛
(4) (4)
If you are given an IVP, use the initial condition to find the particular solution. إذا كنت أعطي IVP استخدام الشرط الأولي للعثور على حل. Note that it may happen that the particular solution is one of the constant solutions given in (1). لاحظ أن ذلك قد يحدث وخصوصا ان الحل هو واحد من حلول ثابتة في (1). This is why Step 3 is important. ولهذا السبب من المهم الخطوة 3.
Example: Find the particular solution of مثال : ابحث عن حل لل
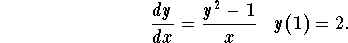
Solution: Perform the following steps: الحل : القيام بالخطوات التالية :
(1) (1)
In order to find the constant solutions, solve من أجل إيجاد حلول المستمر ، لحل
 . We obtain y = 1 and y =-1. ونحن في الحصول على ذ و ذ = 1 =- 1.
. We obtain y = 1 and y =-1. ونحن في الحصول على ذ و ذ = 1 =- 1. (2) (2)
Rewrite the equation as إعادة صياغة المعادلة على النحو
 . .
. . Using the techniques of integration of rational functions , we get باستخدام تقنيات التكامل العقلاني وظائف ، نحصل
 , ،
, ، which implies وهو ما يعني ضمنا

(3) (3)
The solutions to the given differential equation are فإن التوصل إلى حلول في ضوء المعادلة التفاضلية

(4) (4)
Since the constant solutions do not satisfy the initial condition, we are left to find the particular solution among the ones found in (2), that is we need to find the constant C . منذ حلول ثابتة لا تستوفي الشرط الأولي ، فإننا نجد على اليسار وخصوصا تلك التي بين الحل وجدت في (2) ، والتي نحن في حاجة إلى إيجاد المستمر جيم. If we plug in the condition y =2 when x =1, we get إذا كنا في حالة سد ذ = 2 س = 1 عندما نحصل
 . .
. . Note that this solution is given in an implicit form. علما أن هذا الحل هو في شكل ضمني. You may be asked to rewrite it in an explicit one. قد يطلب منك إعادة كتابة ذلك في واحدة واضحة. For example, in this case, we have على سبيل المثال ، في هذه الحالة ، لدينا

If you would like more practice, click on Example . إذا كنت تود الحصول على مزيد من الممارسة العملية ، اضغط على مثال.
مثال : البحث عن حلول
 . .
. . Solution: First, we look for the constant solutions, that is, we look for the roots of الحل : أولا ، نحن نبحث عن حلول ثابتة ، أي أن علينا أن نبحث عن جذور

This equation does not have real roots. هذه المعادلة ليس لها جذور حقيقية. Therefore, we do not have constant solutions. ولذلك ، ليس لدينا حلول ثابتة.
The next step will be to look for the non-constant solutions. وستكون الخطوة التالية هي البحث عن حلول غير ثابتة. We proceed by separating the two variables to get نشرع بفصل اثنين من المتغيرات للحصول على
 . .
. . Then we integrate ثم ندمج

Since منذ
 = =
= =  = 1 - = 1 --
= 1 - = 1 -- 
we get نحصل

Therefore, we have لذلك ، لدينا

It is not easy to obtain y as a function of t , meaning finding y in an explicit form. فليس من السهل الحصول على ذ كوظيفة من وظائف طن ، مما يعني إيجاد ذ بشكل صريح.
Finally, because there are no constant solutions, all the solutions are given by the implicit equation وأخيرا ، لأنه لا توجد حلول ثابتة ، وجميع الحلول التي قدمها ضمنية المعادلة

منقول من موقع رياضيات العالم









