تاريخ الأعداد الأولية 

The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. It is the predecessor to the modern Sieve of Atkin, which is faster but more complex. The eponymous Sieve of Eratosthenes was created in the 3rd century BC by Eratosthenes, an ancient Greek mathematician.
تشير بعض السجلات التاريخية القديمة إلى معرفة قدماء المصريين لمفهوم الأعداد الأولية ، مع ذلك يظل اليونانيون القدامى أول من أجرى دراسات جدية بشأن هذه الموضوع ، فإقليدس على سبيل المثال أثبت في كتبه لا نهائية الأعداد الأولية ، و إراتوسثينيس وضع طريقة سهلة لحساب الأعداد الأولية كما سنرى بعد قليل .
القواسم الأولية


Illustration showing that 11 is a prime number while 12 is not.
The fundamental theorem of arithmetic states that every positive integer larger than 1 can be written as a product of one or more primes in a way which is unique except possibly for the order of the prime factors. The same prime factor may occur multiple times. Primes can thus be considered the “basic building blocks” of the natural numbers. For example, we can write

خصائص الأعداد الأولية
لأن جميع الأعداد التي تنتهي ب ( 0 ، 2 ، 4 ، 6 أو 8 ) هي من مضاعفات الاثنين فليست بالتأكيد أوليّة ، والأعداد التي تنتهي ب ( 0 أو 5 ) من مضاعفات الخمسة فليست أولية أيضاً .
اختبارات أولية العدد
هناك أكثر من 15 اختبارا لمعرفة هل عدد معين أولي أم لا وهي :
اختبار ليكاس - ليهمر
اختبار فيرما المتربط بمبرهنة فيرما الصغرى
اختبار فيرما
مبرهنة فيرما الصغرى تبين أنه إذا كان p عدد أولي و a عدد أولي مع p, إذن :
عكس المبرهنة خاطئ, مثلا 561=3×11×17 ليس عدد أولي و مع ذلك بالنسبة لعدد a أولي مع 561, لدينا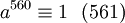
لكن يمكن مع ذلك كتابة:
إذا كان p غير أولي فإن ap − 1 متوافق مع 1 بترديد p لقيمة ما a
الشيء الذي يمثل عكس احتمالي للمبرهنة.
برمجة التشفير PGP, تستعمل هذه الخاصية لمعرفة إذا كانت الأعداد العشوائية التي يختارها أعداد أولية. إذا كان: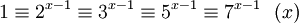 , فهذا يعني أن x عدد أولي احتمالي.
, فهذا يعني أن x عدد أولي احتمالي.
إذا أعطت إحدى المعادلات قيمة مخالفة ل1, في هذه الحالة x عدد غير أولي قطعيا.
أهمية واستخدامات الأعداد الأولية
تستعمل الأعداد الأولية في ميدان المعلوميات و خاصة في علم التعمية. و من أشهر التطبيقات التي تستعمل الأعداد الأولية نجد نظام التشفير RSA. لمزيد من المعلومات راجع التشفير و مشكلة التفكيك إلى جداء عوامل أولية.


The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. It is the predecessor to the modern Sieve of Atkin, which is faster but more complex. The eponymous Sieve of Eratosthenes was created in the 3rd century BC by Eratosthenes, an ancient Greek mathematician.
تشير بعض السجلات التاريخية القديمة إلى معرفة قدماء المصريين لمفهوم الأعداد الأولية ، مع ذلك يظل اليونانيون القدامى أول من أجرى دراسات جدية بشأن هذه الموضوع ، فإقليدس على سبيل المثال أثبت في كتبه لا نهائية الأعداد الأولية ، و إراتوسثينيس وضع طريقة سهلة لحساب الأعداد الأولية كما سنرى بعد قليل .
القواسم الأولية


Illustration showing that 11 is a prime number while 12 is not.
The fundamental theorem of arithmetic states that every positive integer larger than 1 can be written as a product of one or more primes in a way which is unique except possibly for the order of the prime factors. The same prime factor may occur multiple times. Primes can thus be considered the “basic building blocks” of the natural numbers. For example, we can write

خصائص الأعداد الأولية
- جميع الأعداد الأولية - عدا 2 و 5 - تنتهي ب 1 ، 3 ، 7 أو 9 لماذا ؟
لأن جميع الأعداد التي تنتهي ب ( 0 ، 2 ، 4 ، 6 أو 8 ) هي من مضاعفات الاثنين فليست بالتأكيد أوليّة ، والأعداد التي تنتهي ب ( 0 أو 5 ) من مضاعفات الخمسة فليست أولية أيضاً .
- إذا كان لدينا عددان صحيحان أ و ب ، ولدينا عدد ثالث ج ، حيث ج عدد أولي . وكان حاصل ضرب العددين ( أ × ب ) يقبل القسمة على العدد ج ، فإن "أ" أو "ب" يقبل القسمة على ج هذه الخاصية تعرف أيضا ً بمبرهنة إقليدس.
اختبارات أولية العدد
هناك أكثر من 15 اختبارا لمعرفة هل عدد معين أولي أم لا وهي :
اختبار ليكاس - ليهمر
اختبار فيرما المتربط بمبرهنة فيرما الصغرى
اختبار فيرما
مبرهنة فيرما الصغرى تبين أنه إذا كان p عدد أولي و a عدد أولي مع p, إذن :

عكس المبرهنة خاطئ, مثلا 561=3×11×17 ليس عدد أولي و مع ذلك بالنسبة لعدد a أولي مع 561, لدينا
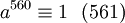
لكن يمكن مع ذلك كتابة:
إذا كان p غير أولي فإن ap − 1 متوافق مع 1 بترديد p لقيمة ما a
الشيء الذي يمثل عكس احتمالي للمبرهنة.
برمجة التشفير PGP, تستعمل هذه الخاصية لمعرفة إذا كانت الأعداد العشوائية التي يختارها أعداد أولية. إذا كان:
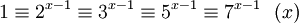 , فهذا يعني أن x عدد أولي احتمالي.
, فهذا يعني أن x عدد أولي احتمالي. إذا أعطت إحدى المعادلات قيمة مخالفة ل1, في هذه الحالة x عدد غير أولي قطعيا.
أهمية واستخدامات الأعداد الأولية
تستعمل الأعداد الأولية في ميدان المعلوميات و خاصة في علم التعمية. و من أشهر التطبيقات التي تستعمل الأعداد الأولية نجد نظام التشفير RSA. لمزيد من المعلومات راجع التشفير و مشكلة التفكيك إلى جداء عوامل أولية.










